UpperHand Gameを作る

コンピュータに相手をさせる(その3)

前回では、min-max法により2手先まで先読みを行うようにしました。でも、3手以上先読みをさせると結構な時間がかかってしまいます。今回はα-β法を使って効率良く先読みを行うように改良します。

α-β法とは

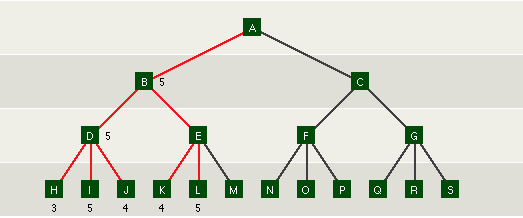
前回のゲームの木をもう一度見てみましょう。 Dの評価値が5と決定した段階でBの評価値は5以下であることが確定します。 Bの評価値はD、Eの最小の評価値となるからです。 Eの評価値が5以上であればBの評価値は5、 Eの評価値が5より小さければBの評価値はその値となります。逆にいうとEの評価値が5以上なることがわかればBの評価値は5となるので、それ以上先読みを行っても無意味ということになります。
実際に先読みを行うと、K、Lの評価値を求めた段階で Mの評価値が何であってもEの評価値が5以上になることがわかります。 Eの評価値はK～Mの最大の評価値となるからです。 Mの評価値を求める必要はなく、Bの評価値は5となりました。

α-β法(βカット)

さらに、Fの評価値が4と決定した段階でCの評価値は4以下であることが確定します。 Bの評価値はすでに5と確定しているので、Cとなる手は決して選ばれないからです。

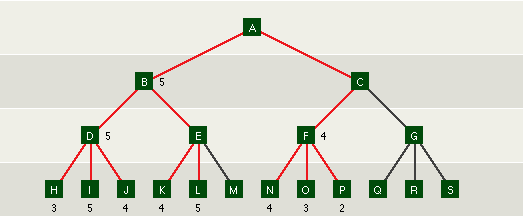
α-β法(αカット)

このようにα-β法では先読みを行う必要のない手の枝刈りを行うことで、効率良く先読みを行っていきます。

α-β法の理屈はわかりましたが、プログラムにするためにはもう少し定式化して理解しておいた方がよいでしょう。
α-β法では各節点(図の四角の部分)の評価値の最小値をα、最大値をβと呼びます。これを(α, β)と書くことにしましょう。この(α, β)を範囲とみなして、範囲外の節点を先読みの対象からはずすという作業を行っていきます。

最初、各節点の範囲は(-∞, +∞)です。 Dの評価値が5と確定した段階でBの評価値は5以下となるので範囲は(-∞, 5)となります。 K、Lの評価値を求めた段階でEの評価値は5以上となるので範囲は(5, +∞)となります。 Eの範囲はBの範囲外となったので先読みの対象からはずします。そしてAの範囲は(5, +∞)となります。このようにある節点の範囲が最大値(β)より大きくなったため先読みの対象からはずすことをβカットといいます。
次に、Fの評価値が4と確定した段階でCの範囲は(-∞, 4)となります。すでにAの範囲は(5, +∞)となっているので Cの範囲は範囲外となり、先読みの対象からはずします。このようにある節点の範囲が最小値(α)より小さくなったため先読みの対象からはずすことをαカットといいます。

α-β法で最高に効率良く枝刈りを行った場合、実際に評価を行う節点の数は先読みの深さを半分としてmin-max法で評価を行う節点の数と同程度であることがわかっています。
つまり最善の場合、同じ時間でmin-max法の倍の深さの先読みを行なえるわけです。

α-β法を実装する

では、α-β法を実装しましょう。
min-max法を実装していたメソッド evaluate()の引数にα、βを追加し、α-β法を行うように改造します。

//-----------------------------------------------------------------------------
//  private float evaluate(UpperHandGame game, int depth,
//                          float alpha, float beta)
//      gameで与えられたゲームをdepth手分先読みして最大の評価値を返す。
//      自分の手番の場合
//          評価値がbeta以上になることが分かった段階で先読みを打ち切る。
//      相手の手番の場合
//          評価値がalpha以下になることが分かった段階で先読みを打ち切る。
//-----------------------------------------------------------------------------
private float evaluate(UpperHandGame game, int depth, float alpha, float beta)
{
    if (depth == 0 || game.isFinish())
    {                               //  これ以上先読みする必要のない場合
        return evaluate(game);  //  局面の評価値を返す。
    }

    //  さらに先読みを行う場合

    float maxEval = alpha;  //  最大の評価値
    float minEval = beta;   //  最小の評価値

    int moves[] = game.moves();     //  着手可能な手を取得する。
    boolean myMove = game.nextPlayer() == player;

    //  着手可能な手の中から優先順位の高い順に先読みを行う。
    for (int i = 0; i < priorityOfMove.length; i++)
    {
        for (int j = 0; j < moves.length; j++)
        {
            if (priorityOfMove[i] == moves[j])
            {
                UpperHandGame newGame = (UpperHandGame)game.clone();
                                                //  局面を複製する。
                newGame.makeMove(moves[j]);     //  着手してみる。
                float eval = evaluate(newGame, depth - 1, maxEval, minEval);
                                                //  着手後の局面を評価する。
                if (myMove)
                {               // 自分の手番の場合
                    if (eval >= beta)
                    {
                        return beta;    //  βカット
                    }
                    maxEval = eval > maxEval ? eval : maxEval;
                }
                else
                {               // 相手の手番の場合
                    if (eval <= alpha)
                    {
                        return alpha;   //  αカット
                    }
                    minEval = eval < minEval ? eval : minEval;
                }
            }
        }
    }

    return myMove ? maxEval : minEval;
}

自分の手番の場合、min-max法では先読みを行った評価値の中で最大の値をその局面の評価値としていましたが、 α-β法ではβの値以上の評価値の局面が見つかった段階で先読みを中断し、 βをその局面の評価値としています(βカット)。
相手の手番の場合は、min-max法では先読みを行った評価値の中で最小の値をその局面の評価値としていましたが、 α-β法ではαの値以下の評価値の局面が見つかった段階で先読みを中断し、 αをその局面の評価値とします(αカット)。

selectMove()ではαの初期値を0(最小の評価値)、 βの初期値を55(最大の評価値)として evaluate()呼び出すようにしています。

//-----------------------------------------------------------------------------
//  public int selectMove(UpperHandGame game)
//      gameから着手する位置を選択し返す。
//-----------------------------------------------------------------------------
public int selectMove(UpperHandGame game)
{
    //  先読みの深さを得る。
    int depth = depth(game);

    if (depth == 0)
    {                       //  先読みしない場合
        ...
    }

    //  先読みする場合

    float maxEval = 0f;     //  最高の評価値
    float minEval = 55f;    //  最低の評価値
    int p = -1;             //  最高の評価の手

    int moves[] = game.moves();         //  着手可能な手を取得する。

    //  着手可能な手の中から優先順位の高い順に先読みを行う。
    for (int i = 0; i < priorityOfMove.length; i++)
    {
        for (int j = 0; j < moves.length; j++)
        {
            if (priorityOfMove[i] == moves[j])
            {
                UpperHandGame newGame = (UpperHandGame)game.clone();
                                                //  局面を複製する。
                newGame.makeMove(moves[j]);     //  着手してみる。
                float eval = evaluate(newGame, depth - 1, maxEval, minEval);
                                                //  着手後の局面を評価する。
                if (eval > maxEval)
                {               //  評価値が最も高い場合。
                    maxEval = eval; //  現在の評価値を最高の評価値とする。
                    p = moves[j];   //  現在の手を最高の評価の手とする。
                }
            }
        }
     }

    return p;   //  最高の評価の手を返す。
}

先読みの深さを変える

α-β法が実装できたので、もう少し先読みを深く行うようにしましょう。
まず、UpperHandクラスのクラス変数PlayerNameに "Master"、"Senior Master" を追加しました。

//-----------------------------------------------------------------------------
//  クラス変数定義
//-----------------------------------------------------------------------------
    ...

//  プレーヤーの名前
private final static String playerName[] = {
                                "You",
                                "Beginer",
                                "Middle Class",
                                "Junior Master",
                                "Master",
                                "Senior Master"
                            };

次に、UpperHandPlayerクラスのメソッドdepth() を変更しました。

//-----------------------------------------------------------------------------
//  private int depth(UpperHandGame game)
//      先読みの深さを返す。
//-----------------------------------------------------------------------------
private int depth(UpperHandGame game)
{
    //  残りの玉の数を得る。
    int ball =  game.ball(UpperHandGame.FIRST) + 
                game.ball(UpperHandGame.SECOND);
    
    if (ball > 52)
    {       //  最初の2手
        return 0;       //  先読みを行わない。
    }
    
    if (rank < 4)
    {       //  Beginer～Masterの場合
        return rank;    //  先読みの深さは固定値とする。
    }
    
    //  残り玉の数に反比例した先読みの深さを返す。
    return 52 * 4 / ball;
}

最初の2手は先読みを行っても手に違いがあらわれないので、先読みを行いません。 Beginer～Masterの場合、 3手目以降は前回までと同様に先読みの深さは固定値としています。 Senior Masterの場合、3手目に4手先を読むようにし、残り玉の数に反比例して先読みの深さが深くなっていくようにしました。

ここまでにできあがったもの

あなたのブラウザはJavaに対応していません。

Javaソースコード (Ver. 1.1a12)

Satoshi Kobayashi (koba@yk.rim.or.jp)