１辺の長さが２の正方形を座標系の上に置きます。
この時、各頂点の座標は(1,1)、(-1,1)、(-1,-1)、(1,-1)となります。
問題は、面積(これはケ−キの分量にあたります。)が３分割されいる上に
周囲の長さ(これはチョコレ−トでコ−ティングされた側面にあたります。)
も３分割されていればいいわけです。
全体の面積は２×２＝４ですから、１人分は(4/3)となります。
全体の周の長さは２×４＝８ですから、１人分は(8/3)となります。
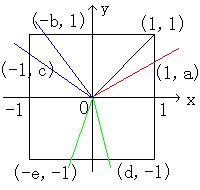切り始めを、原点(0,0)と点(1,a)を結ぶ線分で切るとします。
(０゜〜４５゜で一般化できます。)
２本目のナイフは、点(-1,1)超えるかどうかで場合分けをします。
- (1-a)+2>(8/3)のとき、すなわち(1/3)>aのとき
２本目のナイフは原点(0,0)と点(-b,1)を結ぶ線分で入れるとします。(b>0)
(1-a)+1+b=(8/3)より、b-a=(2/3)
このとき、面積S=1+(1/2)b-(1/2)ａ=1+(1/2)(b-a)=1+(1/2)･(2/3)=(4/3) となり条件に合います。 - (1-a)+2＜(8/3)のとき、すなわち(1/3)＜aのとき
２本目のナイフは原点(0,0)と点(-1,c)を結ぶ線分で入れるとします。(c>0)
(1-a)+2+(1-c)=(8/3)より、a+c=(4/3)
このとき、面積S=2-(1/2)c-(1/2)ａ=2-(1/2)(a+b)=2-(1/2)･(4/3)=(4/3) となり条件に合います。
次に３本目のナイフですが、これは最初に位置から逆回転して
点(0,-1)超えるかどうかで場合分けをします。
- 2+a>(8/3)のとき、すなわちa>(2/3)のとき
３本目のナイフは原点(0,0)と点(d,-1)を結ぶ線分で入れるとします。(d>0)
2+a-d=(8/3)より、a-d=(2/3)
このとき、面積S=1+(1/2)a-(1/2)d=1+(1/2)(a-d)=1+(1/2)･(2/3)=(4/3) となり条件に合います。 - 2+a＜(8/3)のとき、すなわちa＜(2/3)のとき
３本目のナイフは原点(0,0)と点(-e,-1)を結ぶ線分で入れるとします。(e>0)
2+a+e=(8/3)より、a+e=(2/3)
このとき、面積S=1+(1/2)a+(1/2)e=1+(1/2)(a+e)=1+(1/2)･(2/3)=(4/3) となり条件に合います。
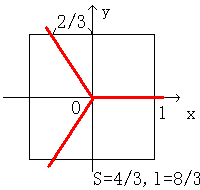
以上の結果をまとめると、どこで切り始めても、
周の長さが(8/3)になるごとにナイフを入れれば、面積も等分されるというわけです。
左の図は０゜の位置から切り始めた時の図です。
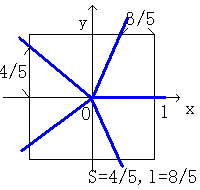
問２．次に、これは３等分に限ったことではないのではないかと思い、 ５等分についてもやってみました。
まず５等分ですが、０゜の位置から切り始めて 周の長さが(8/5)になるごとにナイフを入れていくと、 確かに面積が等分されています。
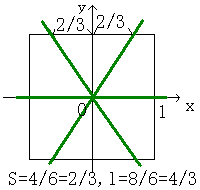
問３．６等分についても同様です。
これを裏付けるためには、周の長さと面積が比例関係にあるということが 証明できればいいわけです。
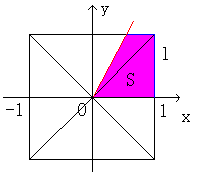
そこで、０゜の位置(実はどこから切りはじめてもいい)の次に
ナイフを入れるところまでの周の長さｌ、
面積Ｓとします。
左の図のように４５゜ずつ切り開くと、
いくつかの三角形の和になります。
高さは常に１、底辺の和は周に長さｌに一致しますから、
常にｌ＝２Ｓという関係がなりたつことがわかります。
周の長さと面積は常に比例関係にあるわけですから、任意の場所から切り始めて、
周の長さが(8/ｎ)になるごとにナイフを入れていくと、
面積も等分されるというわけです。
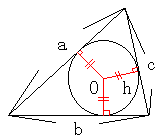
さて次は三角形です。
これも同じように考えられるとしたら、
きっと内心に違いない！ と思ったわけです。
３辺の長さをそれぞれa,b,c、周囲の長さをｌとすると、
l=a+b+cとなります。
三角形の面積Ｓ、内心から各辺までの距離をhとすると、
Ｓ＝(1/2)ah＋(1/2)bh＋(1/2)ch＝(1/2)･h･(a+b+c)＝(1/2)･h･l
となるので、面積Ｓと周囲の長さlが比例関係にあります。
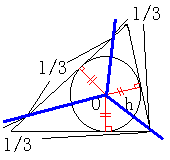
ですから、次のように切ればいいと思います。
必ず内心を通ように切る。
周囲の長さを測り、その1/3になるごとにナイフを入れていく。
これは３等分に限ったことではありませんね。